años
de la carrera de matemáticas en Uniandes
Hace sesenta años la Universidad de los Andes encontró pertinente que un número importante de jóvenes en Colombia se preparase para “investigar, enseñar matemáticas y aplicarlas a diferentes campos”, según recuerda Alberto Schotborgh en su libro sobre la historia del Departamento. Así nació la Carrera de Matemáticas, fuertemente influenciada por John Horváth y Henry Yerly (sus primeros directores), y algunos de sus primeros profesores de planta e invitados ilustres (entre ellos, además de Horváth, Yerly y Schotborgh, matemáticos tan importantes para la época como John von Neumann). El nombre de John Horváth fue sugerido a Mario Laserna por Solomon Lefschetz en los años cincuenta, y su visión durante tal década para el Departamento desembocó en la carrera que hoy, con más de seiscientos egresados, queremos celebrar. La investigación, la enseñanza y la aplicación de las matemáticas en Colombia siguen siendo tareas necesarias e inaplazables, sobre las que hablaremos en los eventos que hemos organizado y en los que queremos encontrar a todos los que han participado en el desarrollo de nuestra carrera. Bienvenidos.
Matemáticas e Inteligencia artificial en Uniandes
Conferencista
Pablo Arbeláez
Director del Centro de Investigación y Formación en Inteligencia Artificial – CinfonIA
Finalizada
60 años de Matemáticas en uniandes
Conferencistas invitados
Jürgen Jost
Director del Max Planck Institute für Mathematik in den Naturwissenschaften, Leipzig, Alemania
Michael Ruzhansky
Director del Ghent Analysis and PDE Center, Bélgica
Sergei Starchenko
Profesor del Department of Mathematics, University of Notre Dame, EE.UU.
Pedro Szekely
Principal Applied Scientist en Amazon Artificial General Intelligence (AGI), EE.UU.
Bernardo Uribe
Profesor del Departamento de Matemáticas de la Universidad del Norte
Conferencistas locales
Carolina Benedetti
Profesora del Departamento de Matemáticas de la Universidad de los Andes
Xavier Caicedo
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Jean Carlos Cortissoz
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Michael Högele
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Nicolás Cuervo Ovalle
Estudiante de Doctorado, Uniandes
Edison Jair Leguizamón
Estudiante de Doctorado, Uniandes
Finalizada
Lógica en Perspectiva
Conferencistas invitados
Sergio Fajardo
Instituto tecnologico de Monterrey
José Lovino
University of Texas at San Antonio
Francisco Miraglia
Universidad de Sao Paulo
Ricardo O. Rodríguez
Universidad de Buenos Aires
Conferencistas locales
Alexander Berenstein
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Carlos Di Prisco
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Luis Jaime Corredor
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Sebastián Rodríguez
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Santiago Pinzón
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Arnold Oostra
Universidad del Tolima
Andrés Villaveces
Universidad Nacional de Colombia
Fernando Zalamea
Universidad Nacional de Colombia
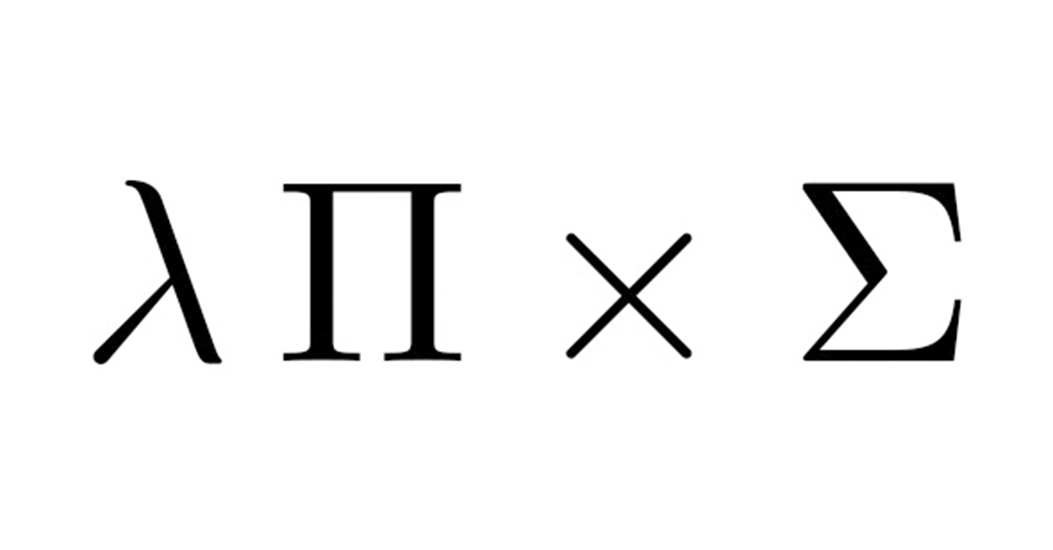
Matemáticas, Lógica e Informática
Conferencistas invitados
Florent Schaffhauser
Mathematisches Institut, Universität Heidelberg, Alemania
Days
:
Hours
:
Minutes
:
Seconds
Beca Yerly
El fondo Henri Yerly lleva más de 20 años premiando la excelencia de los estudiantes en la Carrera de Matemáticas.
Su contribución será fundamental para la construcción de la nueva generación de matemáticos para Colombia.
Hay muchas formas de ayudar:
Donaciones por
PayU
Donaciones por
Nómina
Jürgen Jost
Director del Max Planck Institute für Mathematik in den Naturwissenschaften, Leipzig, Alemania
The Shape of the World
The world comes to us in terms of sensory experiences, physical laws, or data. The challenge for mathematics is to identify general principles and develop formal tools to handle that.
I shall explain with many examples how mathematics has addressed that challenge, culminating in recent research in geometry and machine learning.
Bernardo Uribe
Profesor del Departamento de Matemáticas de la Universidad del Norte
Magnetic Equivariant K-theory
The current research on the topological invariants of magnetic materials, in particular the altermagnets, have made the study of the equivariant K-theory of magnetic space (or Shubnikov) groups necessary. I will present some results on the interesting topological invariants that can be obtained by properly defining the K-theory groups.
Jean Carlos Cortissoz
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Harmonic functions on Riemannian manifolds
In this talk, I will discuss the behavior of harmonic functions on open Riemannian manifolds. To be more precise, my talk will revolve around whether Louville's theorem (i.e. bounded harmonic functions must be constant) and related properties hold in a Riemannian manifold or not.
Michael Ruzhansky
Director del Ghent Analysis and PDE Center, Bélgica
Very weak solutions for evolution PDEs with strong singularities
In this talk we will review the notion of very weak solutions for PDEs with strong singularities, we give example and applications.
Michael Högele
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Observing asymptotic properties in large random graphs
In this talk we present some recent and ongoing research coming from some collaborations from within the department, with my former pregrado student of mathematics Luisa Estrada and more recently my department colleague Tristram Bogart. At the end of the 1950ies Paul Erdös and Alfred Rényi famously classified the topological shapes emerging in a benchmark class of large random graphs according to a hierarchy of scales of the number of edges N = N(n) as a function of the number of vertices n. However, these convergences have not been quantified in the sense of how soon (as a function of n) these shapes are almost surely observable. In collaboration with Luisa Estrada (now U Warwick, UK) and my colleague Alex Steinicke (MU Leoben, AU) we established a quantitative Borel-Cantelli lemma, which turns out to be useful to quantify for instance the emergence of a unique gigantic component accompanied by only isolated points beyond a certain threshold almost surely. This is ongoing work with Tristram Bogart.
Sergei Starchenko
Profesor del Department of Mathematics, University of Notre Dame, EE.UU.
Closure and Hausdorff limits, in tori and nilmanifolds, via o-minimality
In a series of papers, joint with Kobi Peterzil, we began with the following question:
Given a subset X of R^n definable in an o minimal structure, and given a lattice L in R^n, with π from R^n to R^n / L,
what can be said about the closure of π(X) in the torus? A similar question is asked for definable families of sets, and
the Hausdorff limits of their image, in tori and also in nilmanifolds.
Despite the fact that lattices are inherently non-definable in o-minimal structures,
the "flatness of X at infinity" allows us to answer the question using linear spaces associated to the set X.
The goal of the talk is to explain the problem and the answers, using many examples, without a need for model theoretic background.
Pedro Szekely
Egresado Universidad de los Andes
Will Generative AI Change Math Education?
Xavier Caicedo
Profesor del Departamento de Matemáticas de la Universidad de los Andes
0-1 laws beyond first order
The logical 0-1 laws, due independently to Fagin (1976) and Glebskii, Kogan, Ligonkij, Talanov (1969) say, roughly speaking, that the probability that a first order sentence φ is true in a random finite relational structure of power n converges to 0, or converges to 1, as n goes to infinite. Hence, φ is true in almost all finite structures or is false in almost all such structures. We survey the model theoretic aspects of these laws and their possible extension to other logics, including continuous logic.
Carolina Benedetti
Profesora del Departamento de Matemáticas de la Universidad de los Andes
Qué son matroides y dónde encontrarlas
En esta charla iniciaremos un recorrido básico sobre matroides, vistas en distintos ámbitos de la matemática. Mencionaremos su relevancia en la combinatoria algebraica y, al final, hablaremos de resultados recientes en conexión con la geomtería tropical. No se asumirán conocimientos previos en matroides. La charla será en español, con diapositivas en inglés.
What are matroids and where to find them
In this talk we will start with a basic intro to matroids and their appearance in different areas of mathematics. We will explore their significance in algebraic combinatorics and, we finalize with some recent results connecting them with tropical geometry. The talk will be in spanish with slides in english.
Nicolás Cuervo Ovalle
Estudiante de Doctorado del Departamento de Matemáticas de la Universidad de los Andes
El teorema de Ax-Grothendieck
Sea K un campo. Decimos que la función f : K^n → K^n es polinómica si
f(x) = (f1(x), ..., fn(x)) con fi ∈ K[x1, ..., xn] para i = 1, ..., n. En esta charla,
voy a presentar la demostración de un teorema que ha sido mostrado, de manera
independiente, por Ax en y Grothendieck en, que establece lo siguiente:
Teorema 0.1. Toda función polinómica inyectiva f : C^n → C^n es sobreyectiva.
Aunque este resultado se enuncia sobre los números complejos, las demostraciones presentadas originalmente por Ax y Grothendieck no se enfocan tanto en
C, sino en el hecho de que es un cuerpo algebraicamente cerrado de tamaño del continuo.
Además, aunque existen demostraciones dadas por Borel en y Rudin en que utilizan herramientas tanto topológicas como analíticas características de
C, estas resultan ser más técnicas en comparación con las originales. Teniendo
esto en cuenta, reproduciré una demostración basada en los argumentos de Ax
que utilizan herramientas de la teoría de modelos basadas en ultrafiltros
Santiago Gómez Cobos
Estudiante de Doctorado del Department of Mathematics: Analysis, Logic, and Discrete Mathematics, Ghent University.
La influencia de Uniandes en mi formación académica
En esta charla hablaré sobre los elementos del pregrado y maestría en matemáticas de Uniandes que marcaron mi carrera como investigador. Además, presentaré brevemente los temas de investigación que he estado tratando a lo largo de mi doctorado. Concretamente operadores pseudodiferenciales, ecuaciones diferenciales y teoría del índice.
Edison Jair Leguizamon Quinche
Estudiante de Doctorado del Departamento de Matemáticas de la Universidad de los Andes
Teoría de Sturm-Liouville para la construcción de observables.
En los postulados de Dirac-von Neumann, que ofrecen una caracterización matemática de la mecánica cuántica en términos de espacios de Hilbert, se establece que los observables están descritos por operadores auto-adjuntos. Sin embargo, lejos de ser un problema trivial, la construcción de estos operadores puede ser bastante compleja en muchos fenómenos. El objetivo de esta charla es presentar algunos de estos problemas y mostrar cómo se puede aplicar la teoría de Sturm-Liouville para construir operadores asociados a estos fenómenos.
Departamento de Matemáticas
Carrera 1 # 18A - 12
Edificio H
Bogotá Colombia
En caso de ser visitante externo, por favor contactar a
Milton Andres Quintero
601 3394949 EXT. 2716